Abstract
- A unordered collection of Object
- Order and duplicates don’t matter
Notations
Set-Roster Notation
- A Set may be specified by writing all of its Object between braces
- Symbol
...is called ellipsis and read “and so forth”
Set-Builder Notation
- The set of all
xinUsuch thatP(x)is true
Replacement Notation
- For elements x in
A, we apply the functiont(x)
Properties
Membership of a Set
Cardinality of a Set
- The size of the Set
Types of Sets
Subset
Superset
Ais a Subset ofB
Proper Subset
Empty Set
Null Set
Theorem 6.2.4
- Proved using Vacuous Truth of Universal
Singleton
Disjoin Set
- Given 2 Set, both dont have any elements in common
Mutually Disjoin
- Also known as Pairwise Disjoint or Non-overlapping
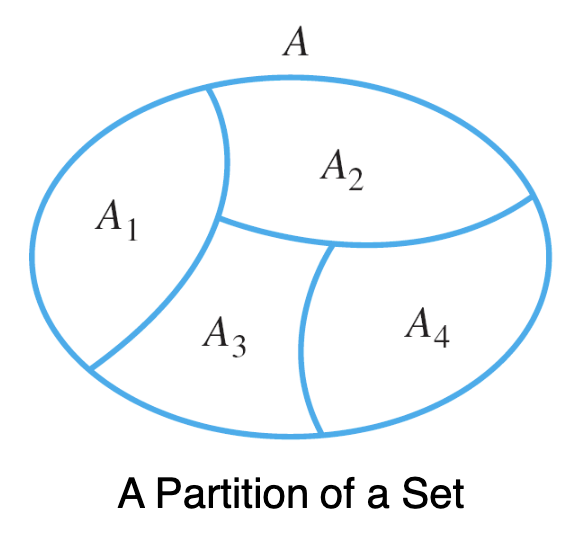
A1,A2,A3,A4are Mutually DisjoinAis called Union of Mutually Disjoint Subsets- The collection of sets is said to be a Partition of
A
Partition
- A partition of Set is a finite or infinite collection of noempty, Mutually Disjoin Subset that can be chained with OR to form
- is one of the mutually disjoin subset, also known as component of the partition
- is the partition
- So basically each isn’t empty, and its elements are not in other mutually disjoin subset
Subset can contain duplicate elements
Given a set ,
is a valid partition
Theorem 8.3.1
-
Two elements are related if and only if they belong to the Mutually Disjoin Subnet in the partition. This connection created by the partition is called the relation induced by the partition
-
Let be a Set with a Partition
-
Let be the relation induced by the partition
-
Then is Reflexive, Symmetric and Transitive
-
For example, imagine dividing students in a class into groups based on their favorite sport. The relation induced by this partition would tell us which students share the same sports preference
Power Set
Theorem 6.3.1
- The cardinality of Superset of finite set is 2 to the power of the cardinality of the finite set
Theorems
Theorem 6.2.1
Inclusion of Intersection
Inclusion in Union
Transitive Property of Subsets
Theorem 6.2.2
- Set Identities
- Very similar to Theorem 2.1.1
- Refer to lecture 5.2.2 for more details
Terminologies
Object
- Members or elements of Set
- Example:
1,2,3{1}are objects in the set of Integer (整数) - It can be either a value or a set
Set Equality
- Given Set
AandB. The Cardinality of a Set must be the same - First way to prove:
- Second way to prove:
Ordered Pair
Order n-tuples
ndenotes the number of Set we are multiplying- Ordered Pair is order 2-tuples, because are multiplying 2 sets
Cartesian Product
- Given Set
AandB, the Cartesian product is a set of Ordered Pair
- Thus
- Cartesian Product of real numbers is basically a set that contains all the possible (x,y) coordinates on the Cartesian Plane
- Depends on the number of set -
n, the Cartesian product is a set of Order n-tuples
